A Briefer History of Time

The forces of Nature and the Unification of Physics

As was explained in Chapter 3, it would be very difficult to construct a complete unified theory of everything in the universe all at one go. So instead we have made progress by finding partial theories that describe a limited range of happenings and by neglecting other effects or approximating them by certain numbers. The laws of science, as we know them at present, contain many numbers— for example, the size of the electric charge of the electron and the ratio of the masses of the proton and the electron—that we cannot, at the moment at least, predict from theory. Instead, we have to find them by observation and then insert them into the equations. Some call these numbers fundamental constants; others call them fudge factors.

Whatever your point of view, the remarkable fact is that the values of these numbers seem to have been very finely adjusted to make possible the development of life. For example, if the electric charge of the electron had been only slightly different, it would have spoiled the balance of the electromagnetic and gravitational force in stars, and either they would have been unable to burn hydrogen and helium or else they would not have exploded. Either way, life could not exist. Ultimately, we would hope to find a complete, consistent, unified theory that would include all these partial theories as approximations and that did not need to be adjusted to fit the facts by picking the values of arbitrary numbers in the theory, such as the strength of the electron’s charge.

The quest for such a theory is known as the unification of physics. Einstein spent most of his later years unsuccessfully searching for a unified theory, but the time was not ripe: there were partial theories for gravity and the electromagnetic force, but very little was known about the nuclear forces. Moreover, as was mentioned in Chapter 9, Einstein refused to believe in the reality of quantum mechanics. Yet it seems that the uncertainty principle is a fundamental feature of the universe we live in. A successful unified theory must, therefore, necessarily incorporate this principle.

The prospects for finding such a theory seem to be much better now because we know so much more about the universe. But we must beware of overconfidence—we have had false dawns before! At the beginning of the twentieth century, for example, it was thought that everything could be explained in terms of the properties of continuous matter, such as elasticity and heat conduction. The discovery of atomic structure and the uncertainty principle put an emphatic end to that. Then again, in 1928 physicist and Nobel Prize winner Max Born told a group of visitors to Göttingen University, "Physics, as we know it, will be over in six months." His confidence was based on the recent discovery by Dirac of the equation that governed the electron. It was thought that a similar equation would govern the proton, which was the only other particle known at the time, and that would be the end of theoretical physics. However, the discovery of the neutron and of nuclear forces knocked that one on its head too. Having said this, there are nevertheless grounds for cautious optimism that we may now be near the end of the search for the ultimate laws of nature.

In quantum mechanics, the forces or interactions between matter particles are all supposed to be carried by particles. What happens is that a matter particle, such as an electron or a quark, emits a force-carrying particle. The recoil from this emission changes the velocity of the matter particle, for the same reason that a cannon rolls back after firing a cannonball. The force-carrying particle then collides with another matter particle and is absorbed, changing the motion of that particle. The net result of the process of emission and absorption is the same as if there had been a force between the two matter particles.

Each force is transmitted by its own distinctive type of force-carrying particle. If the force-carrying particles have a high mass, it will be difficult to produce and exchange them over a large distance, so the forces they carry will have only a short range. On the other hand, if the force-carrying particles have no mass of their own, the forces will be long-range. The force-carrying particles exchanged between matter particles are said to be virtual particles because, unlike real particles, they cannot be directly detected by a particle detector. We know they exist, however, because they do have a measurable effect: they give rise to forces between matter particles.

Force-carrying particles can be grouped into four categories. It should be emphasized that this division into four classes is man-made; it is convenient for the construction of partial theories, but it may not correspond to anything deeper. Ultimately, most physicists hope to find a unified theory that will explain all four forces as different aspects of a single force. Indeed, many would say this is the prime goal of physics today.

The first category is the gravitational force. This force is universal; that is, every particle feels the force of gravity, according to its mass or energy. Gravitational attraction is pictured as being caused by the exchange of virtual particles called gravitons. Gravity is the weakest of the four forces by a long way; it is so weak that we would not notice it at all were it not for two special properties that it has: it can act over large distances, and it is always attractive. This means that the very weak gravitational forces between the individual particles in two large bodies, such as the earth and the sun, can add up to produce a significant force. The other three forces either are short-range or are sometimes attractive and sometimes repulsive, so they tend to cancel out.

The next category is the electromagnetic force, which interacts with electrically charged particles such as electrons and quarks, but not with uncharged particles such as neutrinos. It is much stronger than the gravitational force: the electromagnetic force between two electrons is about a million million million million million million million (1 with forty-two zeros after it) times bigger than the gravitational force. However, there are two kinds of electric charge: positive and negative. The force between two positive charges is repulsive, as is the force between two negative charges, but the force is attractive between a positive and a negative charge.

A large body, such as the earth or the sun, contains nearly equal numbers of positive and negative charges. Thus, the attractive and repulsive forces between the individual particles nearly cancel each other out, and there is very little net electromagnetic force. However, on the small scales of atoms and molecules, electromagnetic forces dominate. The electromagnetic attraction between negatively charged electrons and positively charged protons in the nucleus causes the electrons to orbit the nucleus of the atom, just as gravitational attraction causes the earth to orbit the sun. The electromagnetic attraction is pictured as being caused by the exchange of large numbers of virtual particles called photons. Again, the photons that are exchanged are virtual particles. However, when an electron changes from one orbit to another one nearer to the nucleus, energy is released and a real photon is emitted—which can be observed as visible light by the human eye, if it has the right wavelength, or by a photon detector such as photographic film. Equally, if a real photon collides with an atom, it may move an electron from an orbit nearer the nucleus to one farther away. This uses up the energy of the photon, so it is absorbed.

The third category is called the weak nuclear force. We do not come in direct contact with this force in everyday life. It is, however, responsible for radioactivity—the decay of atomic nuclei. The weak nuclear force was not well understood until 1967, when Abdus Salam at Imperial College, London, and Steven Weinberg at Harvard both proposed theories that unified this interaction with the electromagnetic force, just as Maxwell had unified electricity and magnetism about a hundred years earlier. The predictions of the theory agreed so well with experiment that in 1979, Salam and Weinberg were awarded the Nobel Prize for physics, together with Sheldon Glashow, also at Harvard, who had suggested similar unified theories of the electromagnetic and weak nuclear forces.

The fourth category is the strongest of the four forces, the strong nuclear force. This is another force with which we don’t have direct contact, but it is the force that holds most of our everyday world together. It is responsible for binding the quarks together inside the proton and neutron and for holding the protons and neutrons together in the nucleus of an atom. Without the strong force, the electric repulsion between the positively charged protons would blow apart every atomic nucleus in the universe except those of hydrogen gas, whose nuclei consist of single protons. It is believed that this force is carried by a particle, called the gluon, which interacts only with itself and with the quarks.

The success of the unification of the electromagnetic and weak nuclear forces led to a number of attempts to combine these two forces with the strong nuclear force into what is called a grand unified theory (or GUT). This title is rather an exaggeration: the resultant theories are not all that grand, nor are they fully unified, as they do not include gravity. They are also not really complete theories, because they contain a number of parameters whose values cannot be predicted from the theory but have to be chosen to fit in with experiment. Nevertheless, they may be a step toward a complete, fully unified theory.

The main difficulty in finding a theory that unifies gravity with the other forces is that the theory of gravity—general relativity—is the only one that is not a quantum theory: it does not take into account the uncertainty principle. Yet because the partial theories of the other forces depend on quantum mechanics in an essential way, unifying gravity with the other theories would require finding a way to incorporate that principle into general relativity. But no one has yet been able to come up with a quantum theory of gravity.

The reason a quantum theory of gravity has proven so hard to create has to do with the fact that the uncertainty principle means that even "empty" space is filled with pairs of virtual particles and antiparticles. If it weren’t—if "empty" space were really completely empty— that would mean that all the fields, such as the gravitational and electromagnetic fields, would have to be exactly zero. However, the value of a field and its rate of change with time are like the position and velocity (i.e., change of position) of a particle: the uncertainty principle implies that the more accurately one knows one of these quantities, the less accurately one can know the other. So if a field in empty space were fixed at exactly zero, then it would have both a precise value (zero) and a precise rate of change (also zero), in violation of that principle. Thus there must be a certain minimum amount of uncertainty, or quantum fluctuations, in the value of the field.

One can think of these fluctuations as pairs of particles that appear together at some time, move apart, and then come together again and annihilate each other. They are virtual particles, like the particles that carry the forces: unlike real particles, they cannot be observed directly with a particle detector. However, their indirect effects, such as small changes in the energy of electron orbits, can be measured, and these data agree with the theoretical predictions to a remarkable degree of accuracy. In the case of fluctuations of the electromagnetic field, these particles are virtual photons, and in the case of fluctuations of the gravitational field, they are virtual gravitons. In the case of fluctuations of the weak and strong force fields, however, the virtual pairs are pairs of matter particles, such as electrons or quarks, and their antiparticles.

The problem is that the virtual particles have energy. In fact, because there are an infinite number of virtual pairs, they would have an infinite amount of energy and, therefore, by Einstein’s equation E=mc 2 (see Chapter 5) they would have an infinite amount of mass. According to general relativity, this means that their gravity would curve the universe to an infinitely small size. That obviously does not happen! Similar seemingly absurd infinities occur in the other partial theories—those of the strong, weak, and electromagnetic forces— but in all these cases a process called renormalization can remove the infinities, which is why we have been able to create quantum theories of those forces.

Renormalization involves introducing new infinities that have the effect of canceling the infinities that arise in the theory. However, they need not cancel exactly. We can choose the new infinities so as to leave small remainders. These small remainders are called the renormalized quantities in the theory.

Although in practice this technique is rather dubious mathematically, it does seem to work, and it has been used with the theories of the strong, weak, and electromagnetic forces to make predictions that agree with observations to an extraordinary degree of accuracy. Renormalization has a serious drawback from the point of view of trying to find a complete theory, though, because it means that the actual values of the masses and the strengths of the forces cannot be predicted from the theory but have to be chosen to fit the observations. Unfortunately, in attempting to use renormalization to remove the quantum infinities from general relativity, we have only two quantities that can be adjusted: the strength of gravity and the value of the cosmological constant, the term Einstein introduced into his equations because he believed that the universe was not expanding (see Chapter 7). As it turns out, adjusting these is not sufficient to remove all the infinities. We are therefore left with a quantum theory of gravity that seems to predict that certain quantities, such as the curvature of space-time, are really infinite—yet these quantities can be observed and measured to be perfectly finite!

That this would be a problem in combining general relativity and the uncertainty principle had been suspected for some time but was finally confirmed by detailed calculations in 1972. Four years later, a possible solution, called supergravity, was suggested. Unfortunately, the calculations required to find out whether or not there were any infinities left uncanceled in supergravity were so long and difficult that no one was prepared to undertake them. Even with a computer, it was reckoned, it would take many years, and the chances were very high that there would be at least one mistake, probably more. Thus we would know we had the right answer only if someone else repeated the calculation and got the same answer, and that did not seem very likely! Still, despite these problems, and the fact that the particles in the supergravity theories did not seem to match the observed particles, most scientists believed that the theory could be altered and was probably the right answer to the problem of unifying gravity with the other forces. Then in 1984 there was a remarkable change of opinion in favor of what are called string theories.

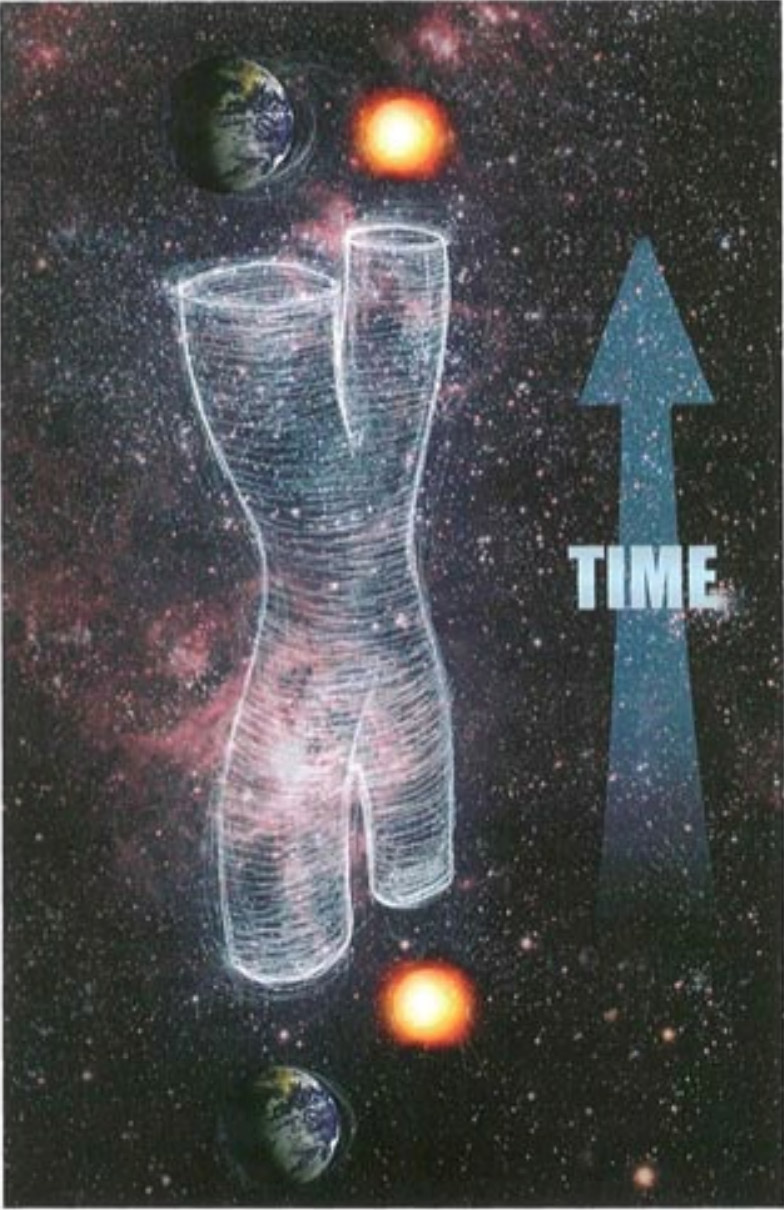
Before string theory, each of the fundamental particles was thought to occupy a single point of space. In string theories, the basic objects are not point particles but things that have a length but no other dimension, like an infinitely thin piece of string. These strings may have ends (so-called open strings) or they may be joined up with themselves in closed loops (closed strings). A particle occupies one point of space at each moment of time. A string, on the other hand, occupies a line in space at each moment of time. Two pieces of string can join together to form a single string; in the case of open strings they simply join at the ends, while in the case of closed strings it is like the two legs joining on a pair of trousers. Similarly, a single piece of string can divide into two strings.

If the fundamental objects in the universe are strings, what are the point particles we seem to observe in our experiments? In string theories, what were previously thought of as different point particles are now pictured as various waves on the string, like waves on a vibrating kite string. Yet the strings, and the vibrations along it, are so tiny that even our best technology cannot resolve their shape, so they behave, in all of our experiments, as tiny, featureless points. Imagine looking at a speck of dust: up close, or under a magnifying glass, you may find that the fleck has an irregular or even stringlike shape, yet from a distance it looks like a featureless dot.

In string theory the emission or absorption of one particle by another corresponds to the dividing or joining together of strings. For example, the gravitational force of the sun on the earth was pictured in particle theories as being caused by the emission of the force-carrying particles called gravitons by a matter particle in the sun and their absorption by a matter particle in the earth. In string theory, this process corresponds to an H-shaped tube or pipe (string theory is rather like plumbing, in a way). The two vertical sides of the H correspond to the particles in the sun and the earth, and the horizontal crossbar corresponds to the graviton that travels between them.

String theory has a curious history. It was originally invented in the late 1960s in an attempt to find a theory to describe the strong force. The idea was that particles such as the proton and the neutron could be regarded as waves on a string. The strong forces between the particles would correspond to pieces of string that went between other bits of string, as in a spiderweb. For this theory to give the observed value of the strong force between particles, the strings had to be like rubber bands with a pull of about ten tons.

In 1974, Joel Scherk from the École Normale Supérieure in Paris and John Schwarz from the California Institute of Technology published a paper in which they showed that string theory could describe the nature of the gravitational force, but only if the tension in the string was about a thousand million million million million million million tons (1 with thirty-nine zeros after it). The predictions of string theory would be just the same as those of general relativity on normal-length scales, but they would differ at very small distances, less than a thousand million million million million millionth of a centimeter (a centimeter divided by 1 with thirty-three zeros after it). Their work did not receive much attention, however, because at just about that time most people abandoned the original string theory of the strong force in favor of the theory based on quarks and gluons, which seemed to fit much better with observations. Scherk died in tragic circumstances (he suffered from diabetes and went into a coma when no one was around to give him an injection of insulin), so Schwarz was left alone as almost the only supporter of string theory, but now with the much higher proposed value of the string tension.

In 1984, interest in strings suddenly revived, apparently for two reasons. One was that people were not really making much progress toward showing that supergravity was finite or that it could explain the kinds of particles that we observe. The other was the publication of another paper by John Schwarz, this time with Mike Green of Queen Mary College, London. This paper showed that string theory might be able to explain the existence of particles that have a built-in left-handedness, like some of the particles that we observe. (The behavior of most particles would be the same if you changed the experimental setup by reflecting it all in a mirror, but the behavior of these particles would change. It is as if they are left- or right-handed, instead of being ambidextrous.) Whatever the reasons, a large number of people soon began to work on string theory, and a new version was developed that seemed as if it might be able to explain the types of particles that we observe.

String theories also lead to infinities, but it is thought that in the right version they will all cancel out (though this is not yet known for certain). String theories, however, have a bigger problem: they seem to be consistent only if space-time has either ten or twenty-six dimensions, instead of the usual four! Of course, extra space-time dimensions are a commonplace of science fiction. Indeed, they provide an ideal way of overcoming the normal restriction of general relativity that one cannot travel faster than light or back in time (see Chapter 10). The idea is to take a shortcut through the extra dimensions. You can picture this in the following way. Imagine that the space we live in has only two dimensions and is curved like the surface of an anchor ring or doughnut. If you were on the inside edge of the ring and you wanted to get to a point across the ring on the other side, you would have to move in a circle along the inner edge of the ring until you reached the target point. However, if you were able to travel in the third dimension, you could leave the ring and cut straight across.

Why don’t we notice all these extra dimensions if they are really there? Why do we see only three space dimensions and one time dimension? The suggestion is that the other dimensions are not like the dimensions we are used to. They are curved up into a space of very small size, something like a million million million million millionth of an inch. This is so small that we just don’t notice it: we see only one time dimension and three space dimensions, in which space-time is fairly flat. To picture how this works, think of the surface of a straw. If you look at it closely, you see the surface is twodimensional. That is, the position of a point on the straw is described by two numbers, the length along the straw and the distance around the circular dimension. But its circular dimension is much smaller than its dimension of length. Because of that, if you look at the straw from a distance, you don’t see the thickness of the straw and it looks one-dimensional. That is, it appears that to specify the position of a point you need only to give the length along the straw. So it is with space-time, string theorists say: on a very small scale it is ten-dimensional and highly curved, but on bigger scales you don’t see the curvature or the extra dimensions.

If this picture is correct, it spells bad news for would-be space travelers: the extra dimensions would be far too small to allow a spaceship through. However, it raises a major problem for scientists as well: why should some, but not all, of the dimensions be curled up into a small ball? Presumably, in the very early universe all the dimensions would have been very curved. Why did one time dimension and three space dimensions flatten out, while the other dimensions remain tightly curled up?

One possible answer is what is called the anthropic principle, which can be paraphrased as "We see the universe the way it is because we exist." There are two versions of the anthropic principle, the weak and the strong. The weak anthropic principle states that in a universe that is large or infinite in space and/or time, the conditions necessary for the development of intelligent life will be met only in certain regions that are limited in space and time. The intelligent beings in these regions should therefore not be surprised if they observe that their locality in the universe satisfies the conditions that are necessary for their existence. It is a bit like a rich person living in a wealthy neighborhood not seeing any poverty.

Some go much further and propose a strong version of the principle. According to this theory, there are either many different universes or many different regions of a single universe, each with its own initial configuration and, perhaps, with its own set of laws of science. In most of these universes the conditions would not be right for the development of complicated organisms; only in the few universes that are like ours would intelligent beings develop and ask the question, "Why is the universe the way we see it?" The answer is then simple: if it had been different, we would not be here!

Few people would quarrel with the validity or utility of the weak anthropic principle, but there are a number of objections that one can raise to the strong anthropic principle as an explanation of the observed state of the universe. For instance, in what sense can all these different universes be said to exist? If they are really separate from each other, what happens in another universe can have no observable consequences in our own universe. We should therefore use the principle of economy and cut them out of the theory. If, on the other hand, they were just different regions of a single universe, the laws of science would have to be the same in each region, because otherwise we could not move continuously from one region to another. In this case the only difference between the regions would be their initial configurations, so the strong anthropic principle would reduce to the weak one.

The anthropic principle gives one possible answer to the question of why the extra dimensions of string theory curled up. Two space dimensions do not seem to be enough to allow for the development of complicated beings like us. For example, two-dimensional animals living on a circle (the surface of a two-dimensional earth) would have to climb over each other in order to get past each other. And if a two-dimensional creature ate something it could not digest completely, it would have to bring up the remains the same way it swallowed them, because if there were a passage right through its body, it would divide the creature into two separate halves: our two-dimensional being would fall apart. Similarly, it is difficult to see how there could be any circulation of the blood in a two-dimensional creature.

There would also be problems with more than three space dimensions. The gravitational force between two bodies would decrease more rapidly with distance than it does in three dimensions. (In three dimensions, the gravitational force drops to one-quarter as you double the distance. In four dimensions it would drop to one-eighth, in five dimensions to one-sixteenth, and so on.) The significance of this is that the orbits of planets, like the earth, around the sun would be unstable: the least disturbance from a circular orbit (such as would be caused by the gravitational attraction of other planets) would result in the earth spiraling away from or into the sun. We would either freeze or be burned up. In fact, the same behavior of gravity with distance in more than three space dimensions means that the sun would not be able to exist in a stable state, with pressure balancing gravity. The sun would either fall apart or collapse to form a black hole. In either case, it would not be of much use as a source of heat and light for life on earth. On a smaller scale, the electrical forces that cause the electrons to orbit around the nucleus in an atom would behave in the same way as gravitational forces. Thus the electrons would either escape from the atom altogether or would spiral into the nucleus. In either case, there would be no atoms as we know them.

It seems clear then that life, at least as we know it, can exist only in regions of space-time in which one time dimension and exactly three space dimensions are not curled up small. This would mean that we could appeal to the weak anthropic principle, provided we could show that string theory does at least allow there to be such regions of the universe—and it seems that indeed string theory does. There may well be other regions of the universe, or other universes (whatever that may mean), in which all the dimensions are curled up small or in which more than four dimensions are nearly flat, but there would be no intelligent beings in such regions to observe the different number of effective dimensions.

In addition to the question of dimensions, another problem with string theory is that there are at least five different theories (two open-string and three different closed-string theories) and millions of ways in which the extra dimensions predicted by string theory could be curled up. Why should just one string theory and one kind of curling-up be picked out? For a time there seemed no answer, and progress got bogged down. Then, starting in about 1994, people started discovering what are called dualities: different string theories and different ways of curling up the extra dimensions could lead to the same results in four dimensions. Moreover, as well as particles, which occupy a single point of space, and strings, which are lines, there were found to be other objects called p-branes, which occupied two-dimensional or higher-dimensional volumes in space. (A particle can be regarded as a 0-brane and a string as a 1-brane, but there were also p-branes for p = 2 to p = 9. A 2-brane can be thought of as something like a two-dimensional membrane. It is harder to picture the higherdimensional branes.) What this seems to indicate is that there is a sort of democracy (in the sense of having equal voices) among supergravity, string, and p-brane theories: they seem to fit together, but none can be said to be more fundamental than the others. Instead they all appear to be different approximations to some more fundamental theory, each valid in different situations.

People have searched for this underlying theory, but without any success so far. It is possible that there may not be any single formulation of the fundamental theory any more than, as Gödel showed, one could formulate arithmetic in terms of a single set of axioms. Instead it may be like maps—you can’t use a single flat map to describe the round surface of the earth or the surface of an anchor ring: you need at least two maps in the case of the earth and four for the anchor ring to cover every point. Each map is valid only in a limited region, but different maps will have a region of overlap. The collection of maps provides a complete description of the surface. Similarly, in physics it may be necessary to use different formulations in different situations, but two different formulations would agree in situations where they can both be applied.

If this is true, the whole collection of different formulations could be regarded as a complete unified theory, though it would be a theory that could not be expressed in terms of a single set of postulates. But even this may be more than nature allows. Is it possible there is no unified theory? Are we perhaps just chasing a mirage? There seem to be three possibilities:

• There really is a complete unified theory (or a collection of overlapping formulations), which we will someday discover if we are smart enough
• There is no ultimate theory of the universe, just an infinite sequence of theories that describe the universe more and more accurately but are never exact
• There is no theory of the universe events cannot be predicted beyond a certain extent but occur in a random and arbitrary manner

Some would argue for the third possibility on the grounds that if there were a complete set of laws, that would infringe God’s freedom to change His mind and intervene in the world. Yet, since God is all-powerful, couldn’t God infringe on His freedom if He wanted to? It’s a bit like the old paradox: can God make a stone so heavy that He can’t lift it? Actually, the idea that God might want to change His mind is an example of the fallacy, pointed out by St. Augustine, of imagining God as a being existing in time. Time is a property only of the universe that God created. Presumably, He knew what He intended when He set it up!

With the advent of quantum mechanics, we have come to recognize that events cannot be predicted with complete accuracy: there is always a degree of uncertainty. If you like, you could ascribe this randomness to the intervention of God. But it would be a very strange kind of intervention, with no evidence that it is directed toward any purpose. Indeed, if it were, it would bv definition not be random. In modern times, we have effectively removed the third possibility above by redefining the goal of science: our aim is to formulate a set of laws that enables us to predict events only up to the limit set by the uncertainty principle.

The second possibility, that there is an infinite sequence of more and more refined theories, is in agreement with all our experience so far. On many occasions we have increased the sensitivity of our measurements or made a new class of observations, only to discover new phenomena that were not predicted by the existing theory, and to account for these we have had to develop a more advanced theory. By studying particles that interact with more and more energy, we might indeed expect to find new layers of structure more basic than the quarks and electrons that we now regard as "elementary" particles.

Gravity may provide a limit to this sequence of "boxes within boxes." If we had a particle with an energy above what is called the Planck energy, its mass would be so concentrated that it would cut itself off from the rest of the universe and form a little black hole. Thus it does seem that the sequence of more and more refined theories should have some limit as we study higher and higher energies, so there should be some ultimate theory of the universe. Yet the Planck energy is a very long way from the energies we can produce in the laboratory at the present time. We shall not bridge that gap with particle accelerators in the foreseeable future. The very early stages of the universe, however, are an arena where such energies must have occurred. There is a good chance that the study of the early universe and the requirements of mathematical consistency will lead us to a complete unified theory within the lifetime of some of us who are around today, always presuming we don’t blow ourselves up first!

What would it mean if we actually did discover the ultimate theory of the universe?

As was explained in Chapter 3, we could never be quite sure that we had indeed found the correct theory, since theories can’t be proved. But if the theory was mathematically consistent and always gave predictions that agreed with observations, we could be reasonably confident that it was the right one. It would bring to an end a long and glorious chapter in the history of humanity’s intellectual struggle to understand the universe. But it would also revolutionize the ordinary person’s understanding of the laws that govern the universe.

In Newton’s time, it was possible for an educated person to have a grasp of the whole of human knowledge, at least in broad strokes. But since then, the pace of the development of science has made this impossible. Because theories are always being changed to account for new observations, they are never properly digested or simplified so that ordinary people can understand them. You have to be a specialist, and even then you can only hope to have a proper grasp of a small proportion of the scientific theories. Further, the rate of progress is so rapid that what you learn at school or university is always a bit out of date. Only a few people can keep up with the rapidly advancing frontier of knowledge, and they have to devote their whole time to it and specialize in a small area. The rest of the population has little idea of the advances that are being made or the excitement they are generating. On the other hand, seventy years ago, if Eddington is to be believed, only two people understood the general theory of relativity. Nowadays tens of thousands of university graduates do, and many millions of people are at least familiar with the idea. If a complete unified theory is discovered, it will be only a matter of time before it becomes digested and simplified in the same way and taught in schools, at least in outline. We will then all be able to have some understanding of the laws that govern the universe and are responsible for our existence.

Even if we do discover a complete unified theory, though, it would not mean that we would be able to predict events in general, for two reasons. The first is the limitation that the uncertainty principle of quantum mechanics sets on our powers of prediction. There is nothing we can do to get around that. In practice, however, this first limitation is less restrictive than the second one. It arises from the fact that we most likely could not solve the equations of such a theory, except in very simple situations. As we’ve said, no one can solve exactly the quantum equations for an atom consisting of a nucleus plus more than one electron. We can’t even solve exactly the motion of three bodies in a theory as simple as Newton’s theory of gravity, and the difficulty increases with the number of bodies and the complexity of the theory. Approximate solutions usually suffice for applications, but they hardly meet the grand expectations aroused by the term "unified theory of everything"!

Today, we already know the laws that govern the behavior of matter under all but the most extreme conditions. In particular, we know the basic laws that underlie all of chemistry and biology. Yet we have certainly not reduced these subjects to the status of solved problems. And we ha\ had, as yet, little success in predicting human behavior from mathematical equations! So even if we do find a complete set of basic laws, there will still be in the years ahead the intellectually challenging task of developing better approximation methods so that we can make useful predictions of the probable outcomes in complicated and realistic situations. A complete, consistent, unified theory is only the first step: our goal is a complete understanding of the events around us, and of our own existence.