A Briefer History of Time

Relativity

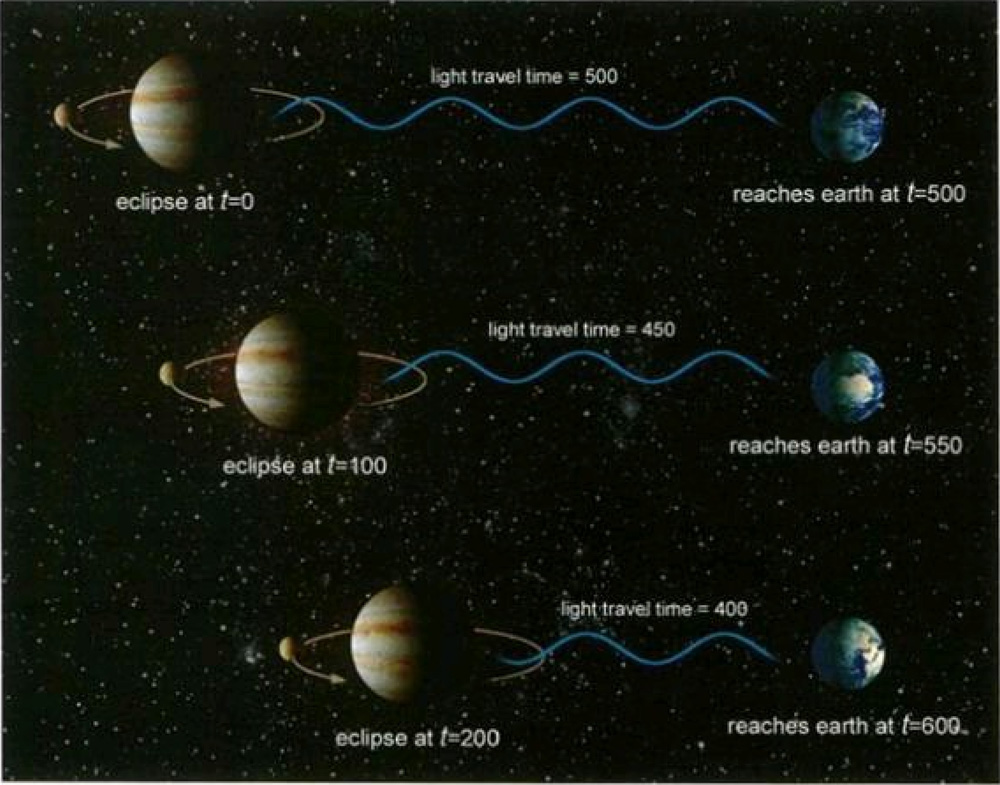
The face that light travels at a finite but very high speed was first discovered in 1676 by the Danish astronomer Ole Christensen Roemer. If you observe the moons of Jupiter, you will notice that from time to time they disappear from sight because they pass behind the giant planet. These eclipses of Jupiter’s moons ought to occur at regular intervals, but Roemer observed that the eclipses were not evenly spaced. Did the moons somehow speed up and slow down in their orbits? He had another explanation. If light traveled with infinite speed, then we on earth would see the eclipses at regular intervals, at exactly the same time that they occurred, like the ticks of a cosmic clock. Since light would traverse any distance instantaneously, this situation would not change if Jupiter moved closer to the earth or further from it.

Now imagine that light travels with finite speed. If so, we will see each eclipse some time after it happened. This delay depends upon the speed of light and on the distance of Jupiter from the earth. If Jupiter did not change its distance from the earth, the delay would be the same for every eclipse. However, Jupiter sometimes moves closer to the earth. In such cases, the "signal" from each successive eclipse has less and less distance to travel, so it arrives progressively earlier than if Jupiter had remained at a constant distance. For analogous reasons, when Jupiter is receding from the earth, we see the eclipses progressively later. The degree of this early and late arrival depends upon the speed of light, and this allows us to measure it. This is what Roemer did. He noticed that eclipses of one of Jupiter’s moons appeared earlier at those times of year when the earth was approaching Jupiter’s orbit and later at those times when the earth was moving away, and he used this difference to calculate the speed of light. However, his measurements of the variations in the distance of the earth from Jupiter were not very accurate, so his value for the speed of light was 140,000 miles per second, compared to the modern value of 186,000 miles per second. Nevertheless, Roemer’s achievement, not only in proving that light travels at a finite speed but also in measuring that speed, was remarkable, coming as it did eleven years before Newton’s publication of Principia Mathematica.

A proper theory of the propagation of light didn’t come until 1865, when the British physicist James Clerk Maxwell succeeded in unifying the partial theories that up to then had been used to describe the forces of electricity and magnetism. Though both electricity and magnetism had been known since ancient times, it wasn’t until the eighteenth century that British chemist Henry Cavendish and French physicist Charles-Augustin de Coulomb established quantitative laws governing the electric force between two charged bodies. A few decades later, in the early nineteenth century, a number of physicists established analogous laws for magnetic forces. Maxwell showed mathematically that these electric and magnetic forces do not arise from particles acting directly on each other; rather, every electric charge and current creates a field, in the surrounding space that exerts a force on every other charge and current located within that space. He found that a single field carries the electric and magnetic forces; thus, electricity and magnetism are inseparable aspects of the same force. He called that force the electromagnetic force, and the field that carries it the electromagnetic field.

Maxwell’s equations predicted that there could be wavelike disturbances in the electromagnetic field and that these waves would travel at a fixed speed, like ripples on a pond. When he calculated this speed, he found it to match exactly the speed of light! Today we know that Maxwell’s waves are visible to the human eye as light when they have a wavelength of between forty and eighty millionths of a centimeter. (A wave is a succession of crests and troughs; the wavelength is the distance between wave crests or troughs.) Waves with wavelengths shorter than those of visible light are now known as ultraviolet light, X-rays, and gamma rays. Waves with longer wavelengths are called radio waves (a meter or more), microwaves (around a centimeter), or infrared radiation (less than one tenthousandth of a centimeter but more than the visible range).

Maxwell’s theory implied that radio or light waves would travel at a certain fixed speed. This was difficult to reconcile with Newton’s theory that there is no absolute standard of rest, because if there is no such standard, there can be no universal agreement on the speed of an object. To understand why, again imagine yourself playing Ping-Pong on the train. If you hit the ball toward the front of the train with a speed your opponent measures to be ten miles per hour, then you’d expect an observer on the platform to perceive the ball moving at one hundred miles per hour—the ten it is moving relative to the train, plus the ninety the train is moving relative to the platform. What is the speed of the ball, ten miles per hour or one hundred? How do you define it— relative to the train or relative to the earth? With no absolute standard of rest, you cannot assign the ball an absolute speed. The same ball could equally well be said to have any speed, depending upon the frame of reference in which the speed is measured. According to Newton’s theory, the same should hold for light. So what does it mean in Maxwell’s theory for light waves to travel at a certain fixed speed?

In order to reconcile Maxwell’s theory with Newton’s laws, it was suggested that there was a substance called the ether that was present everywhere, even in the vacuum of "empty" space. The idea of the ether had a certain added attraction for scientists who felt in any case that, just as water waves require water or sound waves require air, waves of electromagnetic energy must require some medium to carry them. In this view, light waves travel through the ether as sound waves travel through air, and their "speed" as derived from Maxwell’s equations should therefore be measured relative to the ether. Different observers would see light coming toward them at different speeds, but light’s speed relative to the ether would remain fixed.

This idea could be tested. Imagine light emitted from some source. According to the ether theory, the light travels through the ether at the speed of light. If you move toward it through the ether, the speed at which you approach the light will be the sum of the speed of light through the ether and your speed through the ether. The light will approach you faster than if, say, you didn’t move, or you moved in some other direction. Yet because the speed of light is so great compared to the speeds at which we might move toward a light source, this difference in speed was a very difficult effect to measure.

In 1887, Albert Michelson (who later became the first American to receive the Nobel Prize for physics) and Edward Morley carried out a very careful and difficult experiment at the Case School of Applied Science (now Case Western Reserve University) in Cleveland. They realized that because the earth orbits the sun at a speed of nearly twenty miles per second, their lab itself must be moving at a relatively high rate of speed through the ether. Of course, no one knew in which direction or how fast the ether might be moving with respect to the sun, or whether it was moving at all. But by repeating an experiment at different times of the year, when the earth was in different positions along its orbit, they could hope to account for this unknown factor. So Michelson and Morley set up an experiment to compare the speed of light measured in the direction of the earth’s motion through the ether (when we were moving toward the source of the light) to the speed of light at right angles to that motion (when we were not moving toward the source). To their great surprise, they found the speed in both directions was exactly the same!

Between 1887 and 1905, there were several attempts to save the ether theory. The most notable was by the Dutch physicist Hendrik Lorentz, who attempted to explain the result of the MichelsonMorley experiment in terms of objects contracting and clocks slowing down when they moved through the ether. However, in a famous paper in 1905, a hitherto unknown clerk in the Swiss patent office, Albert Einstein, pointed out that the whole idea of an ether was unnecessary, provided one was willing to abandon the idea of absolute time (we’ll see why shortly). A leading French mathematician, Henri Poincaré, made a similar point a few weeks later. Einstein’s arguments were closer to physics than those of Poincaré, who regarded this problem as purely mathematical and to his dying day did not accept Einstein’s interpretation of the theory

Einstein’s fundamental postulate of the theory of relativity, as it was called, stated that the laws of science should be the same for all freely moving observers, no matter what their speed. This was true for Newton’s laws of motion, but now Einstein extended the idea to include Maxwell’s theory. In other words, since Maxwell’s theory dictates that the speed of light has a given value, all freely moving observers must measure that same value, no matter how fast they are moving toward or away from its source. This simple idea certainly explained—without the use of the ether or any other preferred frame of reference—the meaning of the speed of light in Maxwell’s equations, yet it also had some remarkable and often counterintuitive consequences.

For example, the requirement that all observers must agree on how fast light travels forces us to change our concept of time. Picture again the speeding train. In Chapter 4, we saw that although someone on the train bouncing a Ping-Pong ball up and down may say that the ball traveled only a few inches, someone standing on the platform would perceive the ball as traveling about forty meters. Similarly, if the observer on the train shone a flashlight, the two observers would disagree on the distance the light traveled. Since speed is distance divided by time, if they disagree on the distance the light has traveled, the only way for them to agree on the speed of light is for them to also disagree about the time the trip has taken. In other words, the theory of relativity requires us to put an end to the idea of absolute time! Instead, each observer must have his own measure of time, as recorded by a clock carried with him, and identical clocks carried by different observers need not agree.

In relativity there is no need to introduce the idea of an ether, whose presence, as the Michelson- Morley experiment showed, cannot be detected. Instead, the theory of relativity forces us to change fundamentally our ideas of space and time. We must accept that time is not completely separate from and independent of space but is combined with it to form an object called space-time. These are not easy ideas to grasp. Relativity took years to become universally accepted even within the physics community. It is a testament to Einstein’s imagination that he was able to conceive it, and to his confidence in his own logic that he worked out its consequences despite the odd conclusions toward which it seemed to be leading

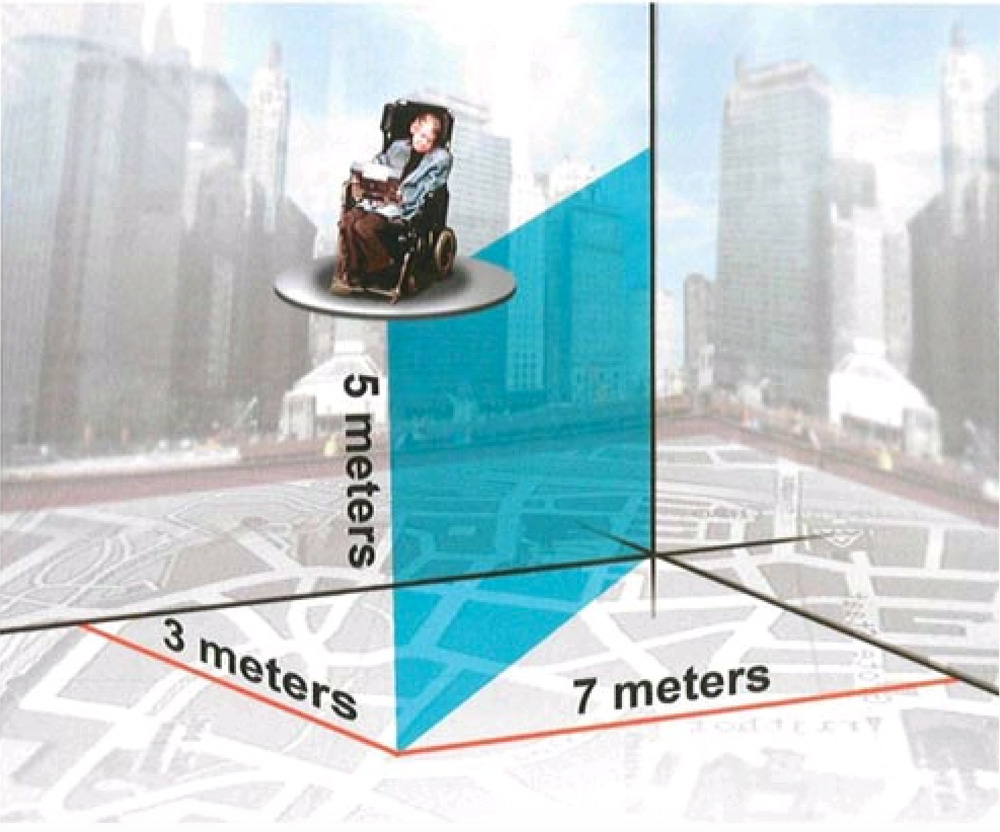
It is a matter of common experience that we can describe the position of a point in space by three numbers, or coordinates. For instance, we can say that a point in a room is seven meters from one wall, three meters from another, and five meters above the floor. Or we could specify that a point is at a certain latitude and longitude and a certain height above sea level. We are free to use any three suitable coordinates, although they have only a limited range of validity. It would not be practical to specify the position of the moon in terms of miles north and miles west of Piccadilly Circus and feet above sea level. Instead, we might describe it in terms of distance from the sun, distance from the plane of the orbits of the planets, and the angle between the line joining the moon to the sun and the line joining the sun to a nearby star such as Proxima Centauri. Even these coordinates would not be of much use in describing the position of the sun in our galaxy or the position of our galaxy in the local group of galaxies. In fact, we may describe the whole universe in terms of a collection of overlapping patches. In each patch, we can use a different set of three coordinates to specify the position of a point.

In the space-time of relativity, any event—that is, anything that happens at a particular point in space and at a particular time—can be specified by four numbers or coordinates. Again, the choice of coordinates is arbitrary: we can use any three well-defined spatial coordinates and any measure of time. But in relativity, there is no real distinction between the space and time coordinates, just as there is no real difference between any two space coordinates. We could choose a new set of coordinates in which, say, the first space coordinate was a combination of the old first and second space coordinates. So instead of measuring the position of a point on the earth in miles north of Piccadilly and miles west of Piccadilly, we could use miles northeast of Piccadilly and miles northwest of Piccadilly. Similarly, we could use a new time coordinate that was the old time (in seconds) plus the distance (in light-seconds) north of Piccadilly

Another well-known consequence of relativity is the equivalence of mass and energy, summed up in Einstein’s famous equation E=mc 2 (where E is energy, m is mass, and c is the speed of light). People often employ this equation to calculate how much energy would be produced if, say, a bit of matter was converted into pure electromagnetic radiation. (Because the speed of light is a large number, the answer is a lot—the weight of matter converted to energy in the bomb that destroyed the city of Hiroshima was less than one ounce.) But the equation also tells us that if the energy of an object increases, so does its mass, that is, its resistance to acceleration, or change in speed.

One form of energy is energy of motion, called kinetic energy. Just as it takes energy to get your car moving, it takes energy to increase the speed of any object. The kinetic energy of a moving object is identical to the energy you must expend in causing it to move. Therefore, the faster an object moves, the more kinetic energy it possesses. But according to the equivalence of energy and mass, kinetic energy adds to an object’s mass, so the faster an object moves, the harder it is to further increase the object’s speed.

This effect is really significant only for objects moving at speeds close to the speed of light. For example, at 10 percent of the speed of light, an object’s mass is only 0.5 percent more than normal, while at 90 percent of the speed of light it would be more than twice its normal mass. As an object approaches the speed of light, its mass rises ever more quickly, so it takes more and more energy to speed it up further. According to the theory of relativity, an object can in fact never reach the speed of light, because by then its mass would have become infinite, and by the equivalence of mass and energy, it would have taken an infinite amount of energy to get it there. This is the reason that any normal object is forever confined by relativity to move at speeds slower than the speed of light. Only light, or other waves that have no intrinsic mass, can move at the speed of light.

Einstein’s 1905 theory of relativity is called special relativity. That is because, though it was very successful in explaining that the speed of light was the same to all observers and in explaining what happens when things move at speeds close to the speed of light, it was inconsistent with the Newtonian theory of gravity. Newton’s theory says that at any given time objects are attracted to each other with a force that depends on the distance between them at that time. This means that if you moved one of the objects, the force on the other one would change instantaneously. If, say, the sun suddenly disappeared, Maxwell’s theory tells us that the earth wouldn’t get dark for about another eight minutes (since that is how long it takes light to reach us from the sun) but, according to Newtonian gravity, the earth would immediately cease to feel the sun’s attraction and fly out of orbit. The gravitational effect of the disappearance of the sun would thus have reached us with infinite speed, instead of at or below the speed of light, as the special theory of relativity required. Einstein made a number of unsuccessful attempts between 1908 and 1914 to find a theory of gravity that was consistent with special relativity. Finally, in 1915, he proposed the even more revolutionary theory we now call the general theory of relativity.